Planning with ants - Alberto Viseras, Rafael Ortiz Losada, Luis Merino, 2016
Abstract
- 빠르게 탐색하는 랜덤 트리(RRT)는 장애물이 많은 환경에서의 경로 계획에 효과적인 것으로 입증되었습니다.
- 이들 방법은 state-space을 균일하게 샘플링하는데, 이는 알고리즘의 완전성을 보장하기 위해 필요하지만 반드시 최적의 해를 찾는 것은 아닙니다.
- 이전 연구에서는 휴리스틱을 사용하여 샘플링 전략을 수정하면 알고리즘 성능이 개선될 수 있음이 보였으나, 이러한 휴리스틱은 최단 경로 계획 문제에만 적용되었습니다.
- 본 연구에서는 사용자 요구에 따라 임의의 휴리스틱을 샘플링 전략에 통합할 수 있는 프레임워크를 제안합니다.
- 이 프레임워크는 ‘경험으로부터 학습하기(learning from experience)’에 기반하는데, 구체적으로 트리 구성에 기여한 샘플의 유용도를 평가하는 유틸리티 함수를 도입하여, 유용도가 높은 위치를 더 자주 샘플링하도록 합니다.
- 이 아이디어를 실현하기 위해 RRT/RRT* 알고리즘에 개미 집단 최적화(ant colony optimization) 개념을 도입하고, 탐사(exploration)와 착취(exploitation)를 균형 있게 조절할 수 있는 새로운 유틸리티 함수를 정의했습니다.
- 또한 anytime구현도 확장했습니다.
- 이 프레임워크는 ‘경험으로부터 학습하기(learning from experience)’에 기반하는데, 구체적으로 트리 구성에 기여한 샘플의 유용도를 평가하는 유틸리티 함수를 도입하여, 유용도가 높은 위치를 더 자주 샘플링하도록 합니다.
- 제안한 방법은 '직사각형 장애물이 여러 개 있는 환경' , '좁은 통로 하나로 구성된 환경' , '미로 형태의 환경' 등 세 가지 시나리오로 검증되었습니다.
- 첫 경로를 찾는 데 걸리는 비용과 시간, 반복 횟수에 따른 경로 품질의 변화를 기준으로 성능을 평가한 결과, 제안된 알고리즘이 기존 최신 RRT 및 RRT* 알고리즘보다 훨씬 뛰어난 성능을 보임을 확인했습니다.

1.Introduction
- 로봇을 initial state에서 goal state로 minimum cost로 이동시키는 optimal path-planning problem는 로봇공학에서 가장 근본적인 문제 중 하나이다.
- 방대한 연구가 이루어졌음에도 불구하고, 이 문제는 여전히 많은 상황에서 도전적입니다.
- 특히, 수색 및 구조 임무나 재난 구호와 같은 생명 안전이 걸린 응용 분야에서는 주어진 시간 내에 최선의 경로를 찾는 것이 목표입니다.
- 이러한 문제를 해결하기 위해, RRT(rapidly exploring random trees)와 같은 샘플링 기반 방법이 널리 사용됩니다.
이 방법은 계산 복잡도가 낮고 효율적으로 해를 찾을 수 있기 때문입니다.
- 하지만 state space을 sampling하는 방식을 변경하면 이 방법의 성능을 더욱 높일 수 있습니다.
- RRT는 일반적으로 상태 공간을 균일하게 샘플링합니다.
- 균일 샘플링(uniform sampling)은 모든 샘플을 동등하게 취급하지만, 대신 어떤 효용 함수( utility function )가 최적화되는 위치에서 새로운 샘플을 선택할 수도 있습니다.
- 따라서 우리는 효용이 높은 위치( high utility location)에서 sampling하는 것을 목표로 하며, 이 utility function는 해를 찾는 데 "걸리는 시간을 최적화"하거나 "이미 찾은 해를 개선"하도록 설계됩니다.
- RRT는 일반적으로 상태 공간을 균일하게 샘플링합니다.
- 본 연구의 목표는 선택한 utility function를 최적화하기 위해 어떻게 샘플링할지에 대한 답을 찾는 것입니다.
- 또한, utility function의 정의를 통해 user requirement에 따라 샘플링 전략을 guide할 수 있는 휴리스틱을 통합하는 프레임워크를 구성할 수 있습니다.
- 이를 통해 기존 RRT* 알고리즘을 미지의 환경에서 정보 기반 경로 계획 및 탐사 응용으로 확장할 수 있습니다.
- 예를 들어, 정보가 더 많은 곳에서 더 자주 샘플링하거나, 사용자의 사전 지식을 활용해 미리 정의된 기준(예: 수색 및 구조 임무에서 험지 회피)을 최적화하는 지능적인 샘플링을 수행할 수 있습니다.
이러한 요소들은 utility function에 쉽게 도입될 수 있습니다.
- 예를 들어, 정보가 더 많은 곳에서 더 자주 샘플링하거나, 사용자의 사전 지식을 활용해 미리 정의된 기준(예: 수색 및 구조 임무에서 험지 회피)을 최적화하는 지능적인 샘플링을 수행할 수 있습니다.
- 하지만 본 연구에서는 최단 경로 계획 문제에 집중하며, 거리 측면에서 경로 비용을 최적화하는 utility function를 설계합니다.
- 알고리즘의 추가 확장 가능성은 결론에서 논의합니다. 머신러닝 기법에서 영감을 받아, 이미 축적된 샘플들을 고려하여 샘플링 전략을 보강합니다.
- 이는 각 순간마다 최적의 샘플링 분포를 나타내는 확률 밀도 함수를 지속적으로 학습하고, 그에 따라 샘플링하는 것으로 해석할 수 있습니다.
- 최적의 샘플링 분포를 결정하기 위해, 우리는 연속 도메인에 대한 개미 군집 최적화(ACO_R)를 사용합니다.
- 알고리즘의 추가 확장 가능성은 결론에서 논의합니다. 머신러닝 기법에서 영감을 받아, 이미 축적된 샘플들을 고려하여 샘플링 전략을 보강합니다.
- ACO_R는 몬테카를로 방법이나 다른 군집 최적화 기법보다 우수한 성능을 보이기 때문에 선택했습니다.
- ACOR 알고리즘은 효용 함수에 따라 가상 개미들을 분포시키고, 이 효용 함수가 개미의 중요도를 평가하여 샘플링 분포를 결정합니다(그림 1 참고).
- 효용 함수는 상태 공간의 활용(즉, 이미 구축된 트리의 최적화)과 상태 공간의 탐사(아직 탐색되지 않은 영역으로 트리의 성장을 유도) 사이의 균형을 맞추도록 설계됩니다.
- 지금까지 구축한 트리를 바탕으로, (i) 샘플이 현재 해를 얼마나 활용하는지, (ii) 샘플이 상태 공간 탐사에 얼마나 기여하는지를 분석합니다.
- 이를 바탕으로 개미들을 업데이트하고, 이로 인해 샘플링 분포와 트리 구축 방식이 변경되어 경로 계획 문제를 해결하게 됩니다.
2. Related work
===> RRT , RRT-Connect , PRM 등 여러 알고리즘 소개
3. Background - Ant colony optimization for continuous domains
- RRT ==> 생략
- RRT* ==> 생략
- ant colony optimization은 어려운 조합 최적화 문제를 해결하기 위해서, 자연에서 영감을 받은 알고리즘이다
- ACO의 원리는 "개미가 먹이를 찾을때 보이는 행동"에서 나온다.
- 1. 개미들은 둥지에서 random한 방향으로 먹이를 찾아 떠난다.
- 2. 개미들이 음식을 찾으면, 그들은 둥지로 돌아가면서 pheromone을 남긴다.
- 3. 이 pheromone의 강도는 먹이의 질과 양에 비례하며 결정되며, 다른 개미들이 이 길을 따라가게 만든다.
- 위와 같은 원리를 연속된 최적화 문제에 적용한것이 연속 도메인 개미 군집 최적화이다.( Ant Colony Optimization fo continuos domains , ACO R )
- ACO_R에서는 각 개미가 가진 utility에 따라서 "어디를 다음 샘플링 지점으로 삼을지"를 결정한다.( 그림 1)
- ( 샘플 추출시에는 가중치 벡터를 기반으로 k개의 개미중에서 하나를 뽑는다. 그리고 해당 개미의 가우시안 확률 밀도 함수로 샘플 1개를 뽑는다.)
- ACO의 원리는 "개미가 먹이를 찾을때 보이는 행동"에서 나온다.

5. 개미 집단 업데이트
- 1. 표 T를 유틸리티 u에 따라서 내림차순으로 정렬한다.
- 2. 새 샘플 X_rand를 개미로 간주해서 T에 삽입한다.
- 3. 만약 X_rand의 utility가 기존 최하위 개미 s_k보다 높다면, 최하위 개미를 제거하여 총 개미 수를 k로 유지한다.
- 4. 위의 과정을 n번 반복 수행
===> 이렇게 함으로써 착취(현재 트리 최적화)와 탐사(새 영역 개척)를 균형 있게 조절하며, 실시간 경로 계획에 적합한 샘플링 분포를 지속적으로 학습하고 적용할 수 있습니다.



4 - 0. ACO-RRT* algorithm
- 본 연구에서는 연속 도메인용 개미 집단 최적화(ACO)를 이용해 샘플링 분포를 수정함으로써 RRT 및 RRT*의 성능을 향상시키는 ACO-RRT* 알고리즘을 제안합니다.
- 우리의 동기는 “경험으로부터 학습”하는 데 있는데, 즉 샘플링 이후 그 샘플이 현재 경로를 얼마나 개선했는지를 평가하고, 이 평가가 다음 샘플 획득 방식에 반영된다는 뜻입니다.
- 알고리즘은 다섯 단계로 구성됩니다(그림 3 참조).
- 개미 초기화: 이후 샘플링에 사용할 개미 집단을 초기화한다.
- 샘플링: 현재 개미들이 정의하는 분포에서 새로운 샘플을 뽑는다.
- 트리 업데이트: 기본 RRT/RRT* 알고리즘에 따라 트리에 새 노드를 추가하고 확장한다.
- 유틸리티 계산: 해당 샘플이
- 현재 솔루션의 착취(exploitation) 측면에서,
- 상태 공간의 탐사(exploration) 측면에서
얼마나 기여했는지를 평가하여 유틸리티 값을 산출한다.
- 개미 업데이트 및 재샘플링: 계산된 유틸리티를 바탕으로 개미 집단을 갱신하고, 수정된 분포에서 다시 샘플링한다.


4 - 1. Initialize ants
- 알고리즘의 첫번째 부분은 k개의 개미로 테이블 T를 채우는 것이다. (알고리즘 3 참고 )
- 1. 장애물이 없는 공간 위에서, 정의된 균일 분포에서 샘플을 뽑는다. (라인 2)
- 2. 해당 샘플의 위치를 l번째 행에 삽입한다. 이때 x_rand ^[j] 는 x_rand의 j번째 차원 좌표를 뜻한다. ( 라인 3,4)
- 3. 유틸리티 u_l을 0으로 초기화한다. ( 알고리즘 표 참고 *** )
4 - 2. Sample ACO

- 이와 같은 샘플링 전략의 변경으로 인해 ACO-RRT* 알고리즘은 이론적으로 RRT*가 보장하는 점근적 최적성(asymptotic optimality)을 엄밀히 보장할 수는 없습니다.
- 그러나 시뮬레이션 결과는 제안된 알고리즘이 최적해에 수렴할 수 있음을 시사합니다.
- 이러한 동작을 설명하는 핵심은 “개미들이 가우시안 확률 밀도 함수와 연관되어 있다”는 사실입니다.
- 가우시안 분포에서 추출된 샘플은 무한한 도메인 전체에 걸쳐 값을 가질 수 있으므로, 상태 공간 전체를 샘플링할 가능성이 열려 있습니다.
- 최악의 경우 모든 개미가 하나의 점으로 수렴하더라도, 각 개미에 연결된 분포의 분산(variance)은 여전히 0보다 약간 큰 값을 유지합니다.
- 이로써 상태 공간 전역이 항상 일정 수준 이상 샘플링되며, 결과적으로 알고리즘이 최적해에 접근할 수 있음을 보장합니다.
4 - 3. Construct tree
- 다음 단계는 기본 RRT 경로 계획 알고리즘에 따라 트리를 구성하는 것입니다.
- 이 단계는 알고리즘 1(RRT)의 4–8번째 줄과 알고리즘 2(RRT*)의 4–23번째 줄에 해당합니다.
- 이 함수는 새 샘플 x_rand와 현재 트리를 입력으로 받고, 트리에 추가된 새 정점 x_new와 갱신된 트리 G를 출력합니다.
- 새 샘플과 현재 트리를 기반으로, "개미들의 상태 공간 샘플링 방식"을 수정할 "유틸리티 함수"를 계산합니다. ( 계산은 4-4에서 설명.)
4 - 4. Calculate utility

4 - 4 - 1. Exploration utility

4 - 4 - 2. Exploitation utility

4 - 4 - 2 - 1. Exploitation utility - No path found


4 - 4 - 2 - 2. Exploitation utility - Path found


4 - 4 - 3. Exploitation utility - Update ants

5. Anytime ACO-RRT*
- ACO-RRT* 알고리즘의 가장 큰 단점은 기본 RRT/RRT*보다 첫 번째 경로를 찾는 데 더 많은 시간이 걸린다는 점입니다.
- 이는 개미들이 초기에 분포를 수렴시키는 데 시간이 필요하기 때문입니다.
- 그러나 한 번 해를 찾으면, 그 해의 품질은 더 우수하여(즉, 비용이 더 작아서) 좋습니다.
- 수색·구조 임무와 같이 첫 해를 빠르게 찾는 것이 중요한 상황이 있습니다.
- 그런 경우 한 번 빠르게 해를 찾고, 시간이 더 주어지면 그것을 개선해 목표에 더 빨리 도달할 수 있다면 이상적입니다.
- Ferguson과 Stentz의 아이디어에서 영감을 받아, 우리는 Anytime ACO-RRT* 알고리즘을 도입합니다.
- 가장 빠른 알고리즘(RRT) 으로 첫 해 TA,B(G)를 빠르게 찾습니다.
- 트리 G(V,E)를 이 첫 해 TA,B(G)로 초기화합니다.
- 그다음 ACO-RRT*를 적용하여, 초기 해를 점진적으로 개선합니다.
- 이 방식은 두 알고리즘의 장점을 결합하여, “빠른 해 탐색”과 “높은 품질의 해”라는 두 마리 토끼를 모두 잡을 수 있게 해 줍니다.

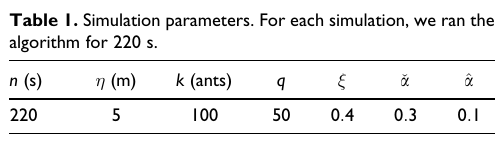
6.Simulations and discussion of results
- 홀로노미컬 로봇을 이용해 세 가지 시뮬레이션 시나리오(그림 5 참조)에서 ACO-RRT* 알고리즘의 성능을 평가했습니다.
- 홀로노미컬 로봇을 선택한 이유는 로봇의 운동학·동역학 제약으로부터 알고리즘의 순수 성능을 분리해 보기 위함입니다.
- 여기서는 로봇을 한 점(point)으로 가정했지만, 더 복잡한 형태의 로봇도 본 프레임워크에 쉽게 적용할 수 있습니다.
- 세 시나리오는 모두 실내 시설 내 네비게이션 중 마주칠 만한 현실적인 환경을 모사하며, 최근의 최첨단 기법들에도 유사한 문제 설정이 사용되었습니다.
- 보다 복잡한 환경이나 운동학·동역학 제약을 고려한 연구는 향후 과제로 남깁니다.
- 모든 시나리오의 크기는 100 m×100 m 이며, 시작점 x_A에서 목표점 x_B로 가는 최적 경로를 찾는 것이 목표입니다.
- 세 번째 시나리오는 미로와 같은 구조를 지녀 초기 위치의 설정이 결과에 큰 영향을 미치므로, 각 시뮬레이션마다 시작점 x_A를 랜덤으로 여러 번 선택해 실험했습니다.
- 또한, 평가 시 목표를 단일 상태가 아닌 목표 영역(goal region)으로 정의했습니다.
- 시나리오 1: 각기 다른 크기의 직사각형 장애물 10개로 구성. 최적 경로 길이는 88 m.
- 시나리오 2: 좁은 통로(narrow passage)를 포함. 경로 계획 문제 중 난도가 높은 환경으로 알려져 있으며, 최적 경로 길이는 63 m.
- 시나리오 3: 미로 같은 구조. 보다 구조화된 환경에서 알고리즘 성능을 검증하기 위해 사용.
- 시뮬레이션은 Intel Xeon E3-1225 @ 3.10 GHz, RAM 8 GB 환경에서 수행했으며, 각 실험은 표 1에 제시된 파라미터를 갖고 100회 반복했습니다.
평가 지표는
- 첫 경로를 찾는 데 걸린 시간 및 그 경로의 비용,
- 시간 흐름에 따른 최적 경로 비용의 진화,
- Anytime 구현의 성능,
- 알고리즘의 다양한 파라미터가 성능에 미치는 영향
등으로 구성되었습니다.

6-1. Time to find first path and associated cost
- 경로 계획 알고리즘 성능을 평가할 때 가장 핵심 지표 중 하나는 첫 번째 경로를 찾는 데 필요한 반복 횟수입니다.
- 이 값은 해당 경로의 비용과도 밀접한 상관관계를 가집니다.
- 그림 6에서는 시나리오 1, 2, 3에 대해 이 두 지표를 모두 평가했습니다. 시나리오 2와 3에서는 실제 시스템에서의 성능을 보여주기 위해 반복 횟수 대신 실제 소요 시간을 사용하여 비교했습니다.
비교 대상은 ACO-RRT*, ACO-RRT, RRT*, RRT 네 가지 알고리즘입니다.
기존 최첨단 알고리즘들과의 직접 비교는 이들이 “가능한 한 빠르게 최적해에 근접”하는 데 초점을 맞추었다는 점에서 본 논문의 목표(“사용자가 정의한 휴리스틱을 학습·적용하여 원 RRT/RRT* 해를 개선”)와 다르므로 수행하지 않았습니다.
그림 6의 박스플롯에서
- 빨간 점선은 중앙값(median),
- 박스의 아래·위 경계는 25⁺ᵗʰ·75⁺ᵗʰ 분위수,
- 수염(whisker)은 최소·최대값 범위를 나타냅니다.
- 관찰 결과, ACO-RRT*는 다른 알고리즘들보다 더 우수한(낮은) 비용의 경로를 찾지만 탐색에는 더 느리게 동작합니다.
- 이는 ACO가 “개미들을 최적 위치로 안착시켜 트리 성장 방향을 잡는” 데 초기 시간이 필요하기 때문입니다.
- 초기 몇 차례 반복 동안 개미들이 적절히 배치되지 않아 시작점과 목표점 사이 경로를 찾지 못하는 반면, 순수 RRT는 첫 경로 탐색 속도가 가장 빠르지만 비용이 가장 높게 나옵니다.
- 이러한 RRT의 빠른 탐색 능력을 Anytime ACO-RRT* 에서 “초기 해 탐색” 단계에 활용합니다.

6-2. Algorithm performance with time
- 첫 경로를 찾은 이후에는 최적해에 도달하도록 해를 지속적으로 개선하는 데 주안점을 둡니다.
- 그림 7은 반복 횟수와 실제 소요 시간에 따른 최적 경로 비용의 변화를 보여 주며, 세 가지 시나리오에 대한 알고리즘 복잡도 시뮬레이션 결과도 함께 제시합니다. 제안된 ACO-RRT* 알고리즘을 ACO-RRT, RRT* 및 RRT와 비교했습니다.
- 그림 7의 각 곡선은 100회 시뮬레이션 실행 결과의 평균값입니다.
- (a), (c), (e) 에서 곡선은 “모든 100회의 실행에서 경로가 최초로 발견된 반복”부터 시작하는 최악의 경우를 기준으로 그렸습니다.
- 관찰 결과, ACO-RRT는 시간이 지남에 따라 다른 기법들보다 더 빠르게(비용 측면에서) 수렴함을 알 수 있습니다.
- 다만 시나리오 3에서는 환경이 미로처럼 구조화되어 있어, 첫 경로를 찾은 후에는 개선 여지가 적으므로 RRT와 유사한 성능을 보입니다.
- 이러한 특성은 “빠르게 첫 해를 찾은 뒤, 시간이 허락하는 한 계속 개선”하는 Anytime ACO-RRT* 알고리즘 설계의 동기가 되었습니다.
- 한편, ACO를 도입하면 개미 유틸리티 계산과 테이블 업데이트에 추가 연산이 필요하기 때문에 계산 복잡도는 다소 증가합니다. 그러나 이러한 추가 비용에도 불구하고 ACO-RRT/RRT*가 제공하는 성능 향상이 이를 충분히 상쇄합니다.
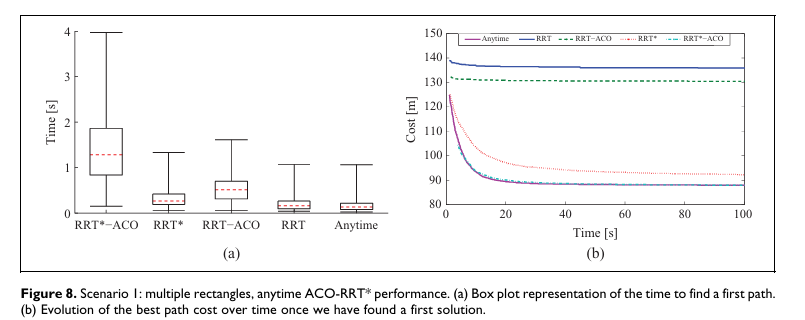
6-3. Anytime ACO-RRT* performance
- 그림 8은 알고리즘의 Anytime 구현 성능을 보여 줍니다.
- 일반적으로 RRT와 Anytime 곡선은 둘 다 RRT로 첫 경로 탐색을 시작하기 때문에 같은 위치에서 시작할 것처럼 보이지만, 여기서는 100회 실행 중 모든 실행이 경로를 찾은 최초 순간을 표시했습니다.
- 실행 횟수가 무한에 가까워지면 두 곡선은 같은 지점에서 시작하게 될 것입니다.
- 결과를 보면, Anytime ACO-RRT* 알고리즘은 첫 경로 탐색 속도가 가장 빠르며(RRT와 동일), 이후 시간에 따른 경로 비용 개선 곡선도 ACO-RRT*와 동일하게 우수한 성능을 보여 줍니다.
-