스냅(snap)
- 궤적의 4차 도함수로써, 시간에 따라서 위치(position) → 속도(velocity) → 가속도(acceleration) → 저크(jerk) → 스냅(snap) 순서로 미분을 한 것.

- 사용이유
- 궤적의 고차 부드러움을 평가하고 제어하기 위해 사용.
- 드론 궤적 최적화에서 minimum - snap기법의 핵심 척도이다.
- 제어 입력 관점
- 쿼드로터 등 기계 시스템은 가속도 명령을 받지만, 실제로는 "가속도의 변화(jerk)"와 "그 변화의 변화(snap)"까지 부드럽게 해주어야, 모터 or 액추에이터가 급격한 토크 변동없이 궤적을 따라갈 수 있다.
- 매끄러움 측정
- snap이 크다는 것은 "가속도가 갑자기 또 크게 바뀐다"는 의미이니, 궤적의 고차원 부드러움을 더 엄격히 제어하려면, snap까지 최소화하는 것이 유리하다.
- 최소-snap 최적화
- 궤적 설계 시 snap의 제곱을 적분한 값을 비용 함수로 삼으면, 제어 입력의 급격한 변화를 억제하면서도, 수치적으로는 볼록 2차 프로그램(Quadratic Program) 형태로 풀수 있다는 장점 존재.
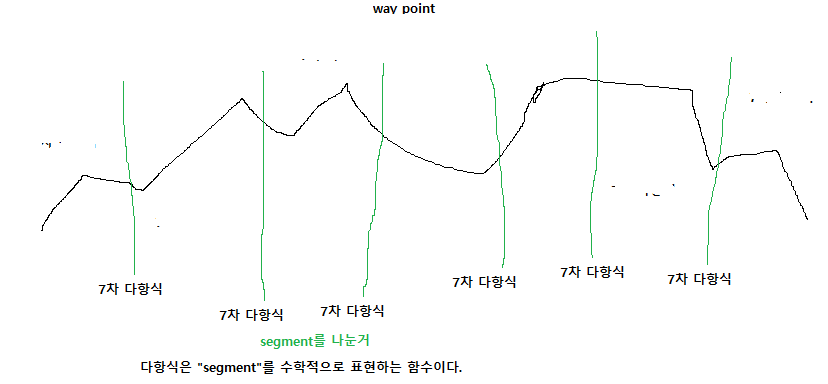
다항식 기반 최소 경로 최적화
- 목표: 주어진 waypoints 집합과 구간별 시간 할당을 만족하면서, 경로의 4차 도함수(snap)의 제곱 적분을 최소화해서, "매끄럽고 동역학적으로 실행 가능한" 경로 계수( 다항식 계수)를 구한다.
- 아래 식에서 T는 적분의 상한( 끝 시간 )이다.

- 기본적인 아이디어
- 로봇이 start -> goal까지의 경로를 움직일때, 각 구간(segment)을 n차 다항식으로 표현한다.
이때, 전체 경로가 부드럽고 자연스럽게 이어지도록, position velocity accerlation jerk snap의 연속성을 보장한다.
- 로봇이 start -> goal까지의 경로를 움직일때, 각 구간(segment)을 n차 다항식으로 표현한다.

- 입력
- 1. 3차원 웨이포인트 { W_0 , W_1 , ... , W_N }
- 2. 각 구간 i별 할당 시간 T_i
- 3. 다항식 차수 n ( 일반적으로 n >= 7 )
- 여기에서 X(t)는 로봇의 상태이다. ( 즉, 경로의 한 축( ex. x좌표 , y좌표 , z좌표 ... )
- 보통 로봇의 경로는 아래의 벡터처럼 표현된다.
- 최적화의 대상은 각각의 다항식 계수이다. 즉, 아래의 벡터를 기준으로 x y z 계수들이며, 전부를 합쳐서 "하나의 큰 최적화 변수 벡터"로 둔다. ( 묶어서 두지만, 실제 최적화에는 각 성분을 따로 다항식으로 풀어서 계산함.)
- 보통 로봇의 경로는 아래의 벡터처럼 표현된다.



위의 식을 풀어보자...
- 1. 경로를 다항식으로 표현
- 경로 X(t)를 각 구간마다 고차 다항식(보통 7차 이상)으로 만든다.

- 2. 4계 도함수 구하기

- 3. 비용 함수 다시 쓰기
- 위의 4계 도함수를 제곱해서, 0부터 T까지 적분한 식을 만든다.
- 아래 식은 다항식 계수 a_4 , a_5 , a_6 ,a_7에 대해서 "이차형식(Quadratic form)"으로 정리한것이다.
- 이차형식에서 a는 계수벡터이며, Q는 비용행렬이다.
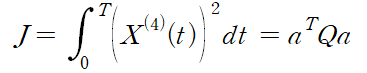
- 4. 경계 조건 / 연속성 등 제약 설정
- 시작점/끝점의 위치,속도,가속도, ... 값을 맞추도록 등식 제약을 추가.
- ex) 시작점/끝점 경계 조건 ==> 궤적의 시작점과 끝점의 위치가 정해져야 함. 만약에 원한다면 고계 도함수까지도 제약
- 시작점/끝점의 위치,속도,가속도, ... 값을 맞추도록 등식 제약을 추가.
- 5. QP ( Quadratic Programming )문제로 만들기
- 6. 해를 구하기
- 7. 여러 구간이라면, 각 구간마다 다항식을 두고, 모든 구간 계수를 하나의 벡터로 합친다. 구간 경계에서의 연속성 제약을 추가
예시



'코딩 및 기타' 카테고리의 다른 글
| Quadratic Program (2) | 2025.07.06 |
|---|---|
| 확률 제약 모델 예측 제어 ( chance - constrained MPC , CC-MPC ) (1) | 2025.07.03 |
| RTAB_MAP시에 imu센서 정보도 더해서 동작 (0) | 2025.06.30 |
| ESDF ( Euclidean Signed Distance Function ) (0) | 2025.06.28 |
| ubuntu opencv install (0) | 2025.06.20 |