[RRT] Improved RRT-Connect Algorithm Based on Triangular Inequality for Robot Path Planning

Improved RRT-Connect Algorithm Based on Triangular Inequality for Robot Path Planning

Improved RRT-Connect Algorithm Based on Triangular Inequality for Robot Path Planning

 

 

0.Abstract

• 본 논문에서는 Triangular inequality기반의 rewiring(리와이어링, 재연결)기법을 빠르게 탐색하는 RRT-Connect에 도입하여, 기존 RRT 알고리즘과 비교했을 때 계획 시간을 보장하면서도 최적에 더 가깝게 만드는 방법을 제안한다.

• 제안된 알고리즘의 성능을 검증하기 위해 다양한 환경에서 시뮬레이션을 통해 RRT 알고리즘과 RRT-Connect 알고리즘을 비교하였다.

  실험 결과, 제안된 알고리즘은 RRT 알고리즘에 비해 더 빠른 계획 시간과 짧은 경로 길이를 보였으며, 샘플 수와 계획 시간이 유사할 때 RRT-Connect 알고리즘보다도 더 짧은 경로 길이를 달성하였다.

 

 

---

 

1. Introduction

• 제4차 산업혁명이 도래함에 따라 로봇 공학, 스마트 팩토리, 자율 주행 등 다양한 분야에서 이동 로봇에 대한 관심이 증가하고 있다[1]. 고전적인 이동 로봇 경로 계획 알고리즘은 크게 세 가지 범주로 분류할 수 있다[2].
  • 첫째는 로드맵 접근법 알고리즘[3]으로, 이동 가능한 경로를 나타내는 지도를 설계하고 이를 통해 경로를 계획하는 방식으로 구현이 용이하다.
  • 둘째는 셀 분할(cell decomposition) 알고리즘[4]로, 구성 공간을 셀 단위로 분할한 뒤 그래프를 이용해 각 셀을 연결하여 경로를 생성한다.
  • 셋째는 인공 퍼텐셜 필드(artificial potential field) 알고리즘[5]로, 인공 퍼텐셜 필드를 생성하고 퍼텐셜의 흐름에 따라 로봇을 목표 지점으로 유도한다.

 

• '최적성(optimality)’은 항상 최적 경로를 보장한다는 의미이고,
  ‘안전 거리(clearance)’는 장애물과 로봇 간의 충돌 확률이 낮음을,
  ‘완전성(completeness)’은 경로가 존재할 경우 반드시 경로를 찾을 수 있음을 뜻한다.
  
  ==> 이러한 고전 알고리즘에서는 최적성, 안전 거리, 완전성이 중요한 연구 주제였으며[6], 특히 알고리즘이 완전성을 보장하지 못하면 유한 시간 내에 경로를 찾지 못하는 치명적인 문제가 발생할 수 있다.

 

• 최근에는 샘플링 기반(path-planning) 알고리즘[7–12], 그중에서도 빠르게 탐색하는 RRT[13]가 고전 알고리즘보다 빠르고 계산 부담이 적어 주목받고 있다.
  • 샘플링 기반 알고리즘의 주요 목적은 '무작위로 추출한 샘플 점(random sampling)'을 이용해 목표 지점으로 빠르게 도달할 수 있는 경로를 찾는 것이다.
    
    고전 알고리즘과 달리 샘플링 기반 알고리즘은 최적성과 완전성을 완전히 보장하기 어렵기 때문에, 대부분 ‘확률적 완전성(probabilistic completeness)’을 주장하며, 이는 무한히 반복되는 샘플링을 통해 확률적으로 완전성에 근접할 수 있다는 의미이다[14].
    ==> 이로 인해 계획 시간(planning time)의 보장과 첫 번째 경로 발견 이후 반복 샘플링을 통해 경로를 최적에 가깝게 수렴시키는 ‘수렴 속도(convergence rate)’를 보장하기 어렵다.
    
    • 특히 동적 환경에서는 계획할 충분한 시간이 주어지지 않을 경우라면, 최적 경로와 차이가 큰 경로가 생성될 수 있다.
      • 그럼에도 샘플링 기반 알고리즘은 고전 알고리즘에 비해 매우 짧은 계획 시간을 제공하여 동적 환경에서 주로 사용된다.

 

• 계획 시간과 수렴 속도의 한계를 극복하기 위해 RRT 알고리즘의 확장을 다룬 연구들이 활발히 진행되고 있다.
  • RRT - Connect 는 start과 goal을 각각 트리의 뿌리(root)로 설정한 뒤, 두 트리를 번갈아 확장함으로써 RRT보다 더 빠르게 경로를 연결한다.
  • 또한 RRT*-smart나 Quick-RRT*[17]와 같이 삼각부등식에 기반해 경로를 최적화하는 알고리즘도 제안되어 최적 경로에 가까운 결과를 도출한다. 이 외에도 다양한 RRT 확장 알고리즘[18–21]이 연구되었다.
  • 그러나 위 알고리즘들은 샘플링 기반 방식의 한계를 어느 정도 극복했음에도 여전히 완전한 최적 경로 산출이 어렵고, 연산량과 소요 시간 측면에서 개선의 여지가 남아 있다.
  • RRT*[18] 알고리즘은 새로 삽입된 노드 주변의 이웃 노드를 탐색(neighbor search)하고, 추가된 경로 길이가 최적화되는 조상 노드(via point)를 찾아 리와이어링(rewiring)하는 과정을 거쳐 RRT보다 짧은 경로를 얻는다.
    • 그러나 이 과정에서 수렴 속도가 개선되는 반면 계획 시간이 크게 증가하는 효율성 trade - off가 발생한다[22].
    • ==> 따라서 RRT*는 계획 시간 및 다른 성능 지표를 모두 고려할 때 항상 RRT보다 우수하다고 할 수 없으며, 계획 시간을 희생하고서야 최적에 접근한다고 볼 수 있다.

 

• 본 논문은 계획 시간을 희생하지 않으면서도 리와이어링을 통해 최적화를 추구하기 위해, RRT-Connect를 기반으로 삼각부등식 원리를 적용한 조상 노드 탐색 방식을 제안한다.
  • 이 방식은 "출발점에서 via point까지의 경로 길이"와 "via point에서 새로 삽입된 노드까지의 경로 길이 합"이 가장 최적화되도록 삼각부등식을 활용하여 경로를 재연결한다.
  • 제안된 알고리즘은 RRT-Connect의 빠른 경로 연결 특성을 유지하면서도 리와이어링을 통해 경로 최적화를 추구하여 계획 시간을 단축한다.
  • 또한 다양한 시뮬레이션 실험을 통해 기존 RRT 및 RRT-Connect 알고리즘과의 성능을 비교·검증하였다.
    • 그 결과, 제안 알고리즘은 샘플 수나 계획 시간을 희생하지 않으면서 RRT 및 RRT-Connect보다 더 짧은 경로를 제공함을 확인하였다.

Figure 1. a는 RRT , b는 RRT-Connect이며 c는 논문에서 제안한 알고리즘이다.

 

• 본 연구의 범위는 "경로를 얼마나 빠르게 찾을 수 있는지"와 "얼마나 더 짧은 경로를 생성할 수 있는지"에 초점을 맞춘다.
  • 동적 환경에서는 네비게이션 가능한 경로를 빠르게 찾는 것이 중요하며, 충분한 수렴 시간이 확보되지 않을 수 있기 때문이다.
  • 즉, 본 논문의 목적은 RRT-Connect 알고리즘을 개선하여 동일한 계획 시간 내에 더 짧은 경로를 찾을 수 있도록 하는 것이다.

 

• figure1은 본 논문에서 다루는 세 가지 주요 알고리즘(RRT, RRT-Connect, 제안 알고리즘)의 개요를 보여준다.
  • 그림 1-a의 RRT는 트리 구조로 확장되는 과정을, 그림 1-b의 RRT-Connect는 출발점과 목표점에서 확장된 두 트리가 서로를 향해 확장되어 연결되는 과정을, 그림 1-c의 제안 알고리즘은 경로 계획 중 RRT-Connect에 삼각부등식 기반의 리와이어링을 적용한 과정을 나타낸다.

 

• 본 논문의 구성은 다음과 같다.
  • 2장에서는 RRT 알고리즘을, 3장에서는 RRT-Connect 알고리즘을 소개하며, 4장에서는 삼각부등식 기반 RRT-Connect 알고리즘을 제안한다.
    • 구체적으로 4.1절에서는 제안된 리와이어링 기법의 의사코드를,
      4.2절에서는 제안 알고리즘의 수학적 모델링을,
      4.3절과 4.4절에서는 제안 기법을 적용한 RRT-Connect 각 단계의 의사코드를, 4.5절에서는 제안 알고리즘의 전체 경로 계획 과정을 설명한다.
    • 5장에서는 실험 환경 및 결과를 제시하고, 6장에서 결론을 맺는다.

 

 

 

---

2. RRT

• figure2-a
  • 1. q_rand를 샘플링하였다.
  • 2. T라는 트리에서 q_rand와 가장 가까운 노드인 q_near을 찾았다.
  • 3. q_rand방향으로 설정해둔 거리만큼 이동한 곳에 q_new를 설정하고, collision check를 하고, collision이 없다면 트리T에 삽입한다.
• figure2-b
  • 위의 과정을 거쳐서 q_goal에 도달하면 최종적인 path가 만들어진다.

 

 

---

3. RRT-Connect

RRT-Connect의 pseudo code

 

---

4 - 0. Proposed Triangular Inequality-Based RRT-Connect Algorithm

• 제안된 삼각부등식 기반 RRT-Connect알고리즘은 RRT-Connect 알고리즘으로 계획된 경로 상의 노드들 사이에 삼각부등식 원리를 적용한 리와이어링 기법으로, 기존 RRT-Connect보다 최적 경로에 더 가깝게 수렴한다.
  • 이는 RRT 알고리즘에 삼각부등식 원리를 적용해 경로를 단축하는 RRT*-Smart[16] 및 Quick-RRT*[17] 알고리즘과 유사하며, 본 논문에서는 이 리와이어링 기법을 ‘Triangular-Rewiring’이라 칭한다.

 

• 제안된 알고리즘은 다음 두 가지 가정을 전제로 한다
  • 1. 출발점(start point)은 하나이며, 목표점(goal point) 역시 하나이지만 시간이 지남에 따라 목표점이 점진적으로 변경될 수 있다.
  • 2. 로봇은 전방향성(omnidirectional) 운동이 가능하다.

 

• 따라서 이 장에서는 먼저 RRT-Connect 알고리즘에 적용할 ‘Triangular-Rewiring’ 기법을 소개하고, 이 기법이 항상 경로를 단축함을 수학적으로 모델링하여 타당성을 검증한다.
  • 검증이 완료되면, ‘Triangular-Rewiring’기법을 RRT-Connect에 실제로 적용하는 방법을 제안한다.
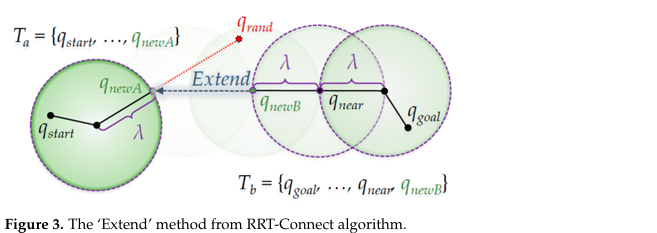
• 구체적으로, 제안된 기법은 3장에서 소개한 RRT-Connect 알고리즘의 주요 절차인 ‘Extend’ 메서드와 ‘Connect’ 메서드에서 새로운 노드를 트리에 삽입할 때마다 적용된다.
• 노드 삽입은 우선 ‘Triangular-Rewiring’기법으로 리와이어링(혹은 적용 여부 결정)을 수행한 뒤 이루어지며, 이 장에서는 이 과정을 반영한 ‘Extend’ 및 ‘Connect’ 메서드의 의사코드를 제시한다.

triangular-rewirig의 의사코드

 

---

 

4 - 1. Pseudocode of the Proposed Triangular-Rewiring Method for the Improved RRT-Connect Algorithm

• ‘Triangular-Rewiring’은 RRT-Connect의 ‘Extend’와 ‘Connect’단계에서 새로운 노드가 삽입될 때마다 호출된다.
• 1. 노드 삽입 준비
  • 1-1. q_new( 혹은 q_newA , q_newB )를 자식 노드( q_child )설정한다.
  • 1-2. 자식노드(q_child)와 연결된 기존 노드(q_near)를 부모 노드 후보(q_parent)로 설정한다.
  • 1-3. q_parent의 부모 노드를 다시 한 단계 위 조상 노드(q_ancestor)로 불러온다.
• 2. 충돌 검사
  • 2-1. isTrapped( q_ancestor , q_child )로 q_ancestor와 q_child사이에 장애물이 있는지 검사한다.
  • 2-2. obstacle이 있으면(참) 리와이어링을 건너뛰고, 기존 RRT-Connect처럼 q_parent를 q_child의 부모로 고정 삽입한다. 장애물이 없으면(거짓) 다음 리와이어링 단계로 진행한다( 다음 단계에서는 triangular-rewiring을 진행 ).
• 3. Triangular - Rewiring 수행
  • 3-1. q_parent와 q_child사이의 간선, 그리고 q_parent와 q_ancestor사이의 간선을 삭제해 기존 연결을 끊는다.
  • 3-2. q_child를 q_ancestor의 자식으로, q_ancestor를 그 위 조상의 자식으로 차례로 재연결한다. (증조할아버지 )
  • 3-3. 다시 isTrapped( q_ancestor , q_child )를 호출하여 장애물 유무를 확인하고, 장애물이 없을 경우 더 높은 조상까지 같은 과정을 반복한다.
  • 3-4. 더 이상 조상이 없거나(=조상이 출발점), 장애물이 발견되면 마지막으로 연결했던 q_parent를 q_child의 부모로 확정 삽입한다.
• ==> 위의 1,2,3과정을 통해서 각 삽입 시점마다 가능한 최단 경로로 리와이어링을 시도한다.

 

 

---

 

4 - 2. Mathematical Modeling of the Proposed Triangular Inequality-Based RRT - Connect Algorithm

• 본절에서는 2차원 유클리드 공간을 가정하여, 제안된 삼각 부등식 기반 RRT-Connect의 수학적 모델링을 소개한다.
  • 제안된 알고리즘은 경로 길이 면에서 RRT-Connect 알고리즘보다 효율적임을 보인다.

 

 

---

 

 

figure 5. triangular-rewiring 방법의 추상과정

식 7,8

• a는 예제 트리
• b는 q_child와 q_ancestor 사이를 rewiring한 후이다.
• c에서 alpha는 q_child와 q_parent사이의 거리이다.
  beta는 q_parent와 q_ancestor사이의 거리이다.
  gamma는 q_child와 q_ancestor사이 거리이다.
  • ==> 다음과 같은 식 성립. α + β ≥ γ 
• 식7,8
  • 이것은 조상 노드사이의 거리 과계를 나타내는 식이다.

 

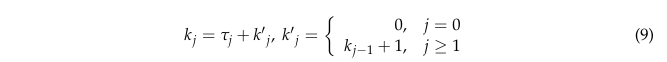
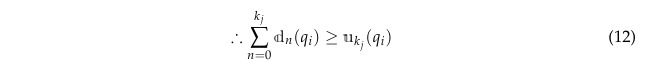
• 식 (9)–(15)는 ‘Triangular-Rewiring’ 기법을 적용한 RRT 알고리즘의 경로가 원래 RRT-Connect 알고리즘이 계획한 경로보다 항상 짧거나 같음을 보인다.
• 식 (9)는 rewiring을 적용했을 때의 거리 u와 적용하지 않았을 때의 거리 d를 비교하기 위한 수열 지표 k_j​를 정의한다.
  • 위에서 j는 u에 대한 수열 인덱스이다.
  • ==> 따라서 k_j도 d에 대한 수열 인덱스이다.
  • τ_j​는 j번째 단계에서 rewiring이 일어난 횟수입니다.
• 식(10)은 임의의 노드 q_i에 대해서, 식1을 일반화하면, rewiring후의 거리를 나타낸다.
  • 위의 그림 5 에서 j=0과 j=1일 때, 각각 한 번씩 rewiring(τ0=1)이 일어나면, 식 (8)의 삼각 부등식 관계를 이용하여, 식11이 성립함을 보일수있다.
  • 그리고 이를 일반화하면 식12가 된다.

 

---

 

4 - 3. Pseudocode of Proposed Extend Method for the Improved RRT-Connect Algorithm

• 이 절에서는 제안된 삼각부등식 기반 RRT-Connect 알고리즘의 ‘Extend’ 메서드(A5)를 소개한다.
  • 제안된 ‘Extend’ 메서드(A5)는 RRT-Connect 알고리즘의 기존 ‘Extend’ 메서드(A3)를 대체한다.
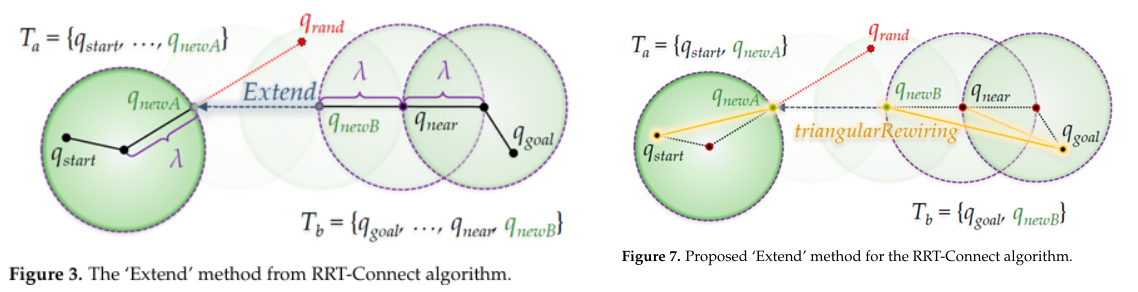
  • 그림 7은 'RRT-Connect 알고리즘의 ‘Extend’ 메서드를 보여주는 그림 3'에 ‘Triangular-Rewiring’ 기법을 적용한 과정을 나타낸다.
    • T_a쪽에서는 q_newA와 q_start가, T_b에서는 T_a로 확장하는 과정에서는 q_near와 q_goal, 그리고 q_newB와 q_goal이 순차적으로 리와이어링된다.
• Algorithm 5는 RRT-Connect 알고리즘의 원래 ‘Extend’ 메서드(A2)에 ‘Triangular-Rewiring’ 기법(A4)을 적용한 것이다.
• 원본 ‘Extend’ 메서드와 비교했을 때, 트리에 노드를 새로 삽입하는 부분(9 행 및 16 행)이 ‘Triangular-Rewiring’ 기법으로 대체된 것 외에는 모두 동일하다.

그림3과 그림7

 

 

---

 

알고리즘 5 , 6

4 - 4. Pseudocode of the Proposed Connect Method for the RRT-Connect Algorithm

• 이 절에서는 제안된 삼각부등식 기반 RRT-Connect 알고리즘의 ‘Connect’ 메서드(A6)를 소개한다.
  • 제안된 ‘Connect’ 메서드(A6)는 RRT-Connect 알고리즘의 기존 ‘Connect’ 메서드(A4)를 대체한다.
• Algorithm 6은 RRT-Connect의 원래 ‘Connect’ 메서드(A3)에 ‘Triangular-Rewiring’ 기법(A4)을 적용한 것이다.
  • 원본 ‘Connect’ 메서드와 비교했을 때, 경로를 병합할 때(5–10행) ‘Triangular-Rewiring’ 기법을 적용하도록 변경된 부분을 제외하면 나머지는 모두 동일하다.

 

• 1.경로 병합
  • P_a와 P_b경로가 트리 구조로 병합되는 시점(5행)에, 병합된 트리 T_merged에 다음 순서로 노드를 삽입한다:
    1. 시작 트리(T_a)의 경로 P_a
    2. 연결 엣지(P_connect)
    3. 목표 트리(T_b)의 경로 P_b
       1. 이때 T_merged의 루트 노드는 q_start가 되며, T_a의 마지막 삽입 노드 q_newA가 n번째로 삽입되면, 그 다음(n+1번째)으로 T_b의 마지막 삽입 노드 q_newB가 들어온다. 최종적으로 q_goal로 삽입을 마친다.
• 2. Triangular-Rewiring 적용
  • 병합된 트리 자체에 ‘Triangular-Rewiring’을 수행한다.
  • 이미 T_a의 extend단계에서 rewiring을 마친 노드는 재검사할 필요가 없으므로, T_merged에 삽입된 노드들 중 q_newA 이후로 삽입된 T_b부분만을 대상으로 rewiring을 진행한다.
    • 구체적으로, q_newA가 i번째 삽입 노드라면, (i+1)번째 노드 pair(q_child, q_parent)부터 시작하여 순차적으로 장애물이 없는지 검사하고, 가능하면 rewiring을 수행한다.
• 3. 종료 조건 및 경로 추출
  • T_merged에 삽입된 모든 노드에 대해 rewiring을 시도한 후, 최종 트리 구조를 경로 P_merged로 변환하고 메서드를 종료(True를 반환).

 

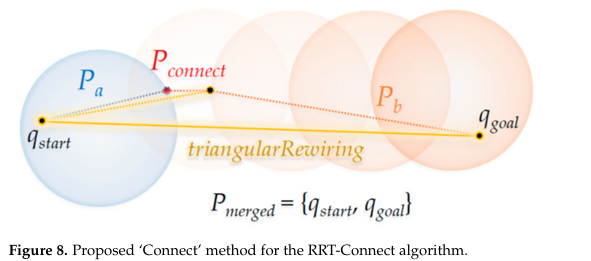
• 그림 8은 RRT-Connect의 ‘Connect’ 메서드(그림 4)에 ‘Triangular-Rewiring’을 적용한 예시를 보여준다.
  • P_a와 P_b가 병합된 뒤(q_start <–> q_goal 사이에 장애물이 없다고 가정) rewiring을 수행하면, 최종적으로 q_start와 q_goal이 가능한 한 직선 경로에 가깝게 연결된 P_merged가 생성된다.

 

 

 

---

4.5. Process of the Proposed Triangular Inequality-Based RRT-Connect Algorithm

그림9. extend와 connect메서드에 triangular-rewiring기법을 적용한 방법이다.

 

 

 

---

 

5. 실험 결과

• 제안된 삼각부등식 기반 RRT-Connect 알고리즘의 성능을 검증하기 위해, 시뮬레이터에서 RRT 알고리즘, RRT-Connect 알고리즘, 그리고 제안한 알고리즘을 여러 환경 지도에서 비교하였다.

 

• 구현 기준
  각 알고리즘은 3장과 4장에 제시된 의사코드(A1–A9)를 바탕으로 구현했으며, RRT 알고리즘의 경우 부록 A에 수록된 의사코드(AA1)를 참고하였다.

 

• 비교용 성능 지표
  1. 샘플 수 (Number of samples)
  2. 경로 길이 (Path length, 픽셀 단위)
  3. 계획 시간 (Planning time, 밀리초 단위)
• 실험 조건
  • 동일한 시작점과 목표점으로 50회 반복 실험(첫 경로 발견 시까지)
  • 스텝 길이(δ) = 30 픽셀
• 지표 해석
  • 샘플 수가 적을수록 동적 환경에서 재계산 비용이 줄어든다.
  • 경로 길이는 경로 계획 알고리즘의 최적성을 나타낸다.
  • 계획 시간은 첫 경로를 찾는 데 걸린 시간이다.

---

 

 

5.1 실험환경

이 절에서는 시뮬레이션에 사용된 환경 지도와 시뮬레이터, 그리고 이를 실행한 컴퓨터 사양을 소개한다.

• 환경 지도
  그림 10에는 본 실험에 사용된 총 8가지 환경 지도가 나타나 있다.
  • 녹색 원(S)은 시작점(start)을, 보라색 원(G)은 목표점(goal)을 표시한다.
  • 노란색(결과 분석 시 파란색)테두리 안의 검은 다각형은 장애물을 의미한다.
  • 모든 지도는 가로 600 픽셀, 세로 600 픽셀 크기이다.
  다양한 장애물 배치와 형태에 따라 알고리즘 성능이 달라지므로, 여러 연구[23–26]에서 다양한 환경 지도를 고려해 왔다.
  본 논문에서는 2017년 한지희[27]가 제안한 벤치마크 환경을 따라 그림 10의 8개 지도를 사용하며, 각 지도는 다음과 같은 특징을 지닌다:
  1. Map 1 (그림 10a)
     – 경로 완전성(completeness) 검증이 용이한 환경.
  2. Map 2 (그림 10b)
     – 경로 완전성이 확인하기 쉽고, 인공 퍼텐셜 필드 알고리즘의 국소 최소(local minima) 문제 해법 예시로 자주 쓰이는 환경.
  3. Map 3 (그림 10c)
     – 최적성(optimality)과 완전성 검증이 쉬우나, 랜덤 샘플링 기반 알고리즘(RRT 등)의 성능이 저하되기 쉬운 구조.
  4. Map 4 (그림 10d)
     – 최적성과 계획 시간(planning time) 검증에 유리하며, 장애물 각도가 복잡해질수록 계산량이 늘어나는 셀 분할(cell decomposition) 방식에는 불리한 환경.
  5. Map 5 (그림 10e)
     – Map 4와 마찬가지로 최적성·계획 시간 검증이 용이하며, 셀 분할 알고리즘에 불리한 환경.
  6. Map 6 (그림 10f)
     – 최적성, 완전성, 계획 시간을 종합적으로 평가하기에 적합한 환경.
  7. Map 7 (그림 10g)
     – 완전성과 최적성 검증이 용이하며, Map 2와 마찬가지로 인공 퍼텐셜 필드 알고리즘 실험에 사용되는 환경.
  8. Map 8 (그림 10h)
     – 완전성과 계획 시간 검증이 쉽지만 RRT 같은 랜덤 샘플링 기반 알고리즘에 불리한 좁은 통로 구조를 가진 환경.
  랜덤 샘플링 기반 알고리즘은 확률적 완전성에 의존하므로, 목표 방향으로 통로가 좁거나 입구가 적을수록 샘플 수와 계획 시간이 크게 증가한다.
• 시뮬레이션 실행 사양
  표 1에는 본 논문 실험에 사용된 컴퓨터 사양을 정리했다.
  • 시뮬레이터는 C#(.NET Framework 4.8.03752, Visual Studio Community 2019 v16.1.6)으로 개발했으며, 시각화 부분을 제외한 모든 연산은 단일 스레드로 처리했다.
  • 따라서 측정된 계획 시간은 컴퓨터 성능에 따라 차이가 날 수 있다.

 

---

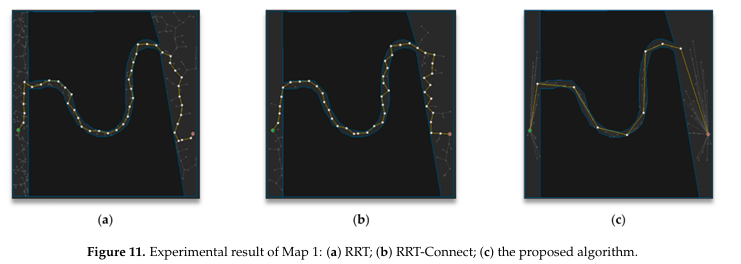
map1에 대한 결과

 

---

map2에 대한 결과

 

---

map3에 대한 결과

---

map8에 대한 결과

 

---

6.결론

• 본 논문에서는 RRT-Connect 알고리즘의 최적성 한계를 극복하기 위해 삼각부등식 원리를 적용한 삼각부등식 기반 RRT-Connect 알고리즘을 제안하였다.
  • 제안된 ‘Triangular-Rewiring’ 기법의 타당성을 수학적으로 검증하고 이를 RRT-Connect에 적용하여 최적 경로에 더 가깝게 수렴하도록 하였다.
  • 또한, 제안 알고리즘의 첫 경로 탐색을 위한 샘플 수, 경로 길이, 계획 시간 등의 성능 지표를 확인하기 위해 8가지 환경에서 RRT 및 RRT-Connect 알고리즘과 비교 실험을 수행하였다.
    • ==>그 결과, 경로 길이 면에서 제안 알고리즘은 RRT 대비 평균 20%, RRT-Connect 대비 평균 16% 효율이 개선되었으며, 계획 시간 면에서는 RRT 대비 평균 47% 더 빠르고 RRT-Connect 대비 평균 2% 느린 성능을 보였다.
      결론적으로 제안 알고리즘은 유사한 샘플 수와 계획 시간을 유지하면서도 RRT-Connect보다 더 짧은 경로를 생성함을 확인하였다.
    • 다만 한계점으로는 Kinodynamic 계획 문제가 있다. ‘Triangular-Rewiring’ 과정에서 중간 노드가 삭제되면 예리한 모서리를 갖는 비미분(piecewise linear) 경로가 발생하여 로봇의 운동학적 제약을 위반할 수 있다.