논문

SMUG Planner: A Safe Multi-Goal Planner for Mobile Robots in Challenging Environments

정지홍 2025. 2. 16. 21:55

[2306.05309] SMUG Planner: A Safe Multi-Goal Planner for Mobile Robots in Challenging Environments

 

SMUG Planner: A Safe Multi-Goal Planner for Mobile Robots in Challenging Environments

Robotic exploration or monitoring missions require mobile robots to autonomously and safely navigate between multiple target locations in potentially challenging environments. Currently, this type of multi-goal mission often relies on humans designing a se

arxiv.org

 

 

 

SMUG Planner란?

  • 위의 논문에서는 도전적인 환경에서 로봇이 안전하게 여러 목표를 방문하는 알고리즘이라고 한다.

 

 

0. abstract

  • 모바일 로봇이 탐험 or 모니터링을 하는 일은 다음을 요구한다.
    • 잠재적으로 도전적인 환경에서, 혼자서 안전하게 여러 목표로 향해서 가야한다.
    • 최근, multi-goal mission은 로봇이 path or waypoint를 따라가는 것은 사람이 만드는 set of actions에 의존했다.
  • 해당 연구에서는, 미리 정의한 목표지점들의 방문에 대한 문제이다. 각각은 다양한 잠재적 위치에서 방문을 할 것이다.
  • 자율성을 증가시키기 위해서, SMUG planner를 제안한다. 이는 목표 방문을 위한 최적의 motion path를 생성한다.
    • 안전성과 효율성을 증가시키기 위해서,  HSVC ( hierarchical state validity checking )  를 제안한다.
      • HSVC를 사용하여, 시뮬레이션에서 학습된 로봇 고유의 주행 가능성을 학습한다.
    • 또한 informed smapler와 함께 Lazy PRM *를 사용한다. ( 이로써 충돌 없는 경로의 생성을 더 빠르게 할수있다 )
      • 우리의 반복적인 dynamic programming 알고리즘은 수초 이내에 1개 이상의 목표지점을 방문하는 경로를 만들어 낼수 있다. 
        게다가 우리가 제안한 HSVC ( hierarchical state validity checking ) 은 planning time을 pure volumetric collision checking보다 30%감소 시겼다. ( 당연히 고위험 지역을 피하면서 안전성을 높였다. ) 
  • 우리는 SMUG planner를 4족 보행로봇인 ANYmal에 배포하였고, 거친환경(rough terrain)에서 다중 목표 미션을 자율적으로 달성하였다.

 

 

fig1

1. Introduction

  • multi-goal mission은 흔히 탐험,검사,시나리오 모니터링에서 자주 보인다.
    • 이러한 종류의 mission에서는, 로봇들은 자세한 조사를 위해서 수많은 관심 목표에 방문한다. 
      ( 예를 든다면, 기기를 배치하거나 샘플 수집 혹인 계측기의 측정값을 읽기 등 )
  • 그러나 현재의 임무에서는 로봇들이 자율적으로 탐색하고 계획할수 있는 능력이 제한되며, 인간의 조작에 의존한다.
  • 우주 탐사에서는 이와같은 multi-goal mission이 흔히 응용된다.
    • 하나의 예로는 ARCHES라는 지질학적 임무이다
    • 또 다른 예시는 ESA와 ESRIC가 시작한 우주 자원 도전이다.
    • 하지만 위의 2가지 예시에서는 아무도 multi-goal planner를 사용하지 않았다.
      그들은 공급된 waypoints에 의해서만 운영되었다.(혹은 휴리스틱을 사용해서 항상 가장 가까운 목표를 방문했다.)
  • 탐사 mission외에도, multi-goal navigation은 산업 점검과 모니터링 작업에도 연관있다.
  • fully autonomous multi-goal mission planner는 아직 없다. 
    즉, 결과적으로 이러한 mission들은 대부분 인간의 조작에 의존하며, 지연을 일으킬수도 있으며 sub-optimal 의사결정 및 효율성에 제한이 존재한다.
  • 그래서 본 논문에서는 SMUG planner를 제안한다.
    • 이는 set of targets에 안전하게 방문하기 위한 경로를 계획하는 multi-goal planner이다. 그리고 해당 경로로 자세한 조사를 수행한다.
    • 우리는 target을 Target of Interest라고 하며, 방문이 가능한 유효 pose를 Pose of Interest라고 한다. ( fig1참고 )
    • 더 정확히말하면, planner는 각ToI당 하나의 PoI를 방문할것이다. 이를 multi-goal mission이라고 언급한다.
      • 이는 경로계획에서 충돌이 없느 일반화된 외판원 문제(GTSP)이다.
      • 문제에 포함된 많은 수의 충돌이 없는 경로로 인해서, GLNS와 같은 기존의 GTSP solver로 해결하는 것은 불가능하다.
        왜냐하면, solver는 모든 충돌이 없는 경로를 계산해야하며, 이는 계산 비용이 너무커서 비실용적이다.
    • 어떻게 안전성을 보장하면서 최적의 경로를 만드는것은 특히 도전할 과제이다.
  • SMUG planner는 2단계의 planning schema를 구현하였다.
    • 1번째는 TSP를 사용하여 ToIs의 방문순서를 최적화 시킨다.
    • 2번째는 각각의 ToI에 대한 PoI를 최적화 시킬건데, 반복적인 Dynamic Programming을 사용 할것이다.
      반복적인 DP를 IDP( iterative dynamic programming )이라고 하자.
    • 충돌이 없는 경로를 생성하기 위해서 informed sampler란? 를 사용한 LazyPRM*를 사용할것이다.
    • 안전한것을 보장하기 위해서, 로봇 고유의 주행 가능성 추정 모듈을 사용해서 계층적 장애물 회피 전략을 제안한다.
      • 이는 로봇이 mission과 onboard deployment에서 경로 재탐색을 할수있게한다.
        SMUG planner는 이러인해서 통신 제약이 존재하는 환경에서도 사용할수있다. ( 이러한 상황은 많은 탐사나 시나리오 모니터링에서 흔하다 )
    • 정리하자면 아래와 같다.
      • 1.  모바일 로봇은 충돌이 없는 경로계획에서 GTSP문제를 푸는 multi-goal planner는 안전한 경로를 10개 이상의 목표에 대해서 몇초만에 빠르게 생성해야한다.
      • 2. 고위험 지역을 피하고 충돌을 체크하는 시간이 기준의 pure volumetric collision checking에 비해서 30% 속도가 감소하였다.
      • 3. 거친환경에서 multi-goal mission를 수행하는 ANYmal 보행로봇에 배포하였다. 우리가 알기로는 충돌이 없는 경로계획을 GTSP로 푸는 것은 이것이 처음일것이다. 

 

 

 

6 . Conclusions

  • 이번 연구에서, 우리는 SMUG planner을 제안하였다.이는 multi-goal planner이며 안전하고 최적화된 경로를 빠르게 생성할수 있으며, 생성한 경로는 다양한 탐험이나 산업의 inspection mission에 맞게 생성된다.
  • 같이 제안한 IDP알고리즘은, planner는 12개의 목표를 방문하는 global path를 generate하는것이 8초만에 가능하며, 이는 순수한 접근 방식보다 8.9배 더 빠르다.
  • 제안한 계층적 state validity checking scheme는 안전성을 향상시키고, 계획 시간을 기존보다 30%줄여주었다.
  • 우리는 ANYmal 로봇으로 실험을 진행하였고, 제안한 planner가 실제로 적용 가능함을 보여주었다.
    • 우리가 알기로는 실시간 GTSP를 수행하는 global planner의 첫번째 사례이다.
  • 우리는 ToIs가 모든 PoIs에 대해서 점검할 수 있다고 추측한다. 하지만 몇몇의 시나리오에서는, 선택된 PoI에 대해서 ToI를 점검할수 없는 경우에 더 많은 대체할 옵션이 필요하다.
  • 해당 planner는 지상 로봇에 대한 것이니, 곧바로 드론과 같은 높은 자유도를 요구하는 로봇에 적용하기는 어려울 것 이다.
    • 하지만 IDP는 해당하는 point-to-point planner가 주어진 경우에는 모든 로봇에 대해서 일반화가 가능하다.
  • 또한, 기본적인 OMPL SE(2)공간은 보행 로봇의 주헹 능력을 반영하지 않는다. 이를 해결하기 위해서, 우리는 간단한 전처리 휴리스틱에 의존하였다. 이는 waypoint의 방향으로 정렬을 해서 로봇이 옆으로 이동하기보다는 앞으로 이동하는 것을 보장한다.
  • 결국에는, 시뮬레이션에서 배운 것을 가지고 더 합리적인 경로 비용은 보행 로봇의 움직임에 맞게 조정되고, 이에 맞는 informed sampler를 사용해서 해결할 수 있다.

 

 

2. Related work

  • 우리는 이전에 연구된 샘플링 기반의 path planning알고리즘과 multi-goal 문제에 대해서 모델링 하는 TSP와 이의 변형을 바탕으로 진행한다.
    실제 환경에 배포하는 것을 목표로 하며, 모바일 로봇에 배포된 기존의 planner에 대해서 리뷰한다.
  • 1. 샘플링 기반의 path planning
    • path planning의  방법중에서 샘플링 기반의 방법이 존재한다. ( 이는 그리드월드 같이 이산화를 사용하지않고, 연속적인 상태 공간을 나타낼수있다.)
      PRM ( probabilistic Roadmap ) 이 존재하며 이를 최적화 한것이 PRM*이다. 
      PRM*는 확률맵을 만들고 서로다른 경로 탐색 요청에서 수집한 정보를 효율적으로 재사용하니, 동일한 환경에서 여러개의 시작-목표 쌍을 계획하는데 적합하다.
      collision-checking of nodes and edges는 비용이 많이들고, 우리의planner는 계산 효율성이 중요하니 LazyPRM*이 적절하다.
      LazyPRM은 최적의 경로를 구성할 가능성이 있는 경우에만 엣지의 유효성을 검사해서 전체적인 계획 시간을 줄여준다. Gammel은 현재까지 발견된 최적의 경로의 비용을 기반으로 샘플링 공간을 제한함으로써 경로 개선 속도를 높이는 방법을 제안했다. 본 논문에서는 LazyPRM을 기반으로하며, 효율적인 multi-goal planner를 위해서 informed sampler를 사용한다.
  • 2. multi-goal sequencing problem
    • TSP는 주어진 목표지점을 최적의 순서로 방문하는 문제이다. 보통의 TSP는 single point의 target을 고려한다.
      이에 반해서 GTSP와 TSPN( tsp with neighborhoods )는 각각 목표를 여러개의 점 집합 or 연속족인 영역으로 고려한다. 
      실제 환경에서는 목표 지점을 정확히 방문하는 것이 아니라, 일정 거리 내에서 접근하는 것으로도 충분한 경우가 많기에, 이러한 접근법이 보다 현실적인 접근 방법이다.
      • GTSP를 풀기 위해서 아래와 같은 방법들이 존재한다.
        • Branch and Cut [18], Lagrangian relaxation [19] or transforming GTSP to an equivalent TSP instance [20]
      • GTSP와 TSPN을 풀기 위해서는 아래와 같은 방법이 존재한다.
        • ant-colony optimization [21], genetic algorithm [22], [23] and Lin-Kernighan heuristic [24] or formulate the problem as Mixed Integer Nonlinear Programming (MINLP) [25].
    • 하지만 위의 연구들은 복잡한 환경에서 이동하는 모발일 로봇의 collision-free path planning에 대한 높은 계산 비용은 고려하지않는다.
      • 이에 대해서 . Alatartsev et al. 은 TSPN를 2개의 subproblems로 나누었다.
        • 1. Given the visiting point of each target, find the optimal visiting sequence문제
        • 2. given the visiting sequence, find the optimal visiting points문제
          • ( 각 목표 지점을 방문할 위치가 주어질때, 최적의 방문 순서를 찾는다 or 방문 순서가 주어질때, 최적의 방문 위치를 찾는 문제. )
        • 그리고 위의 2가지 문제를 반복적으로 해결하는 방식이다.
          본 연구에서는 현실적인 환경에서 필수적인 장애물 회피를 고려하지 않았으나, 문제를 2개의 하위 문제로 나누는 전략은 유용하며, 이를 우리의 방법에 채택한다.
    • Gentilini는 'focuses on combinatorial optimization with Hybrid Random Key Generic Algorithm (HRKGA)'를 다룬다. 하지만 계산비용커서 안쓸거에용
    • GTSP와 TSPN의 변형중에서 collision-free path planning을 ' Multi-Goal Path Planning Problem (MTP)' 과 'MTP for Goal Regions (MTPGR)' 라고 불린다.
      • Gao et al는 MTPGR문제를 Alatartsev et al. 과 겉이 2개의 하위 문제로 나누었다. 하지만 반복적으로 해결하는 대신에, 최적의 방문 순서를 한번만 해결하는 방식을 선택했다. 그리고나서, 목표지점 사이의 경로는 처음에는 직선 경로로 가정한뒤 Rubber Band Algorithm (RBA)를 사용하여, 방문 지점을 조정하면서 경로를 점진적으로 개선하였다. 
        • 즉, 충돌없는 경로는 최적의 global path를 구성할 가능성이 존재할때만 계획되니, 계산할 경로의 수가 크게 줄어든다.
          • 그러나 RBA는 local optimal에 빠질 가능성이 크다. 이는 방문 지점을 조정할때, 오직 인접한 두 경로만 고려하여 조정하기 때문이다. 또한 2d격자 환경에서만 실험했지, 현실에서는 하지 않았다.
      • MTPGR문제를 푸는 대신에 우리는 multi-goal 문제를 MTP로 모델링하기로 했다. 여기에서는 ToIs를 지속적인 neighborhood가 아니라 PoIs집합으로 가정합니다. 왜냐면 ToI를 기기에 배치할때, 특정한 공격 각도나 기타 제약 조건이 요구되어, 유효한 PoI들이 서로 분리되어 나타날수있기 때문이다.
      • 물론 가장 일반적인 선택은 ToI를 neighborhoods와 연결되지 않은 집합으로 모델링하는것이다.(이는 GTSP에 해당됨.)
      • 우리는 각각의 ToI를 이산적인 집합으로 가정하여 문제를 간단히 하면서도, 여전히 유효한 PoI의 제안을 허용한다.
  • 3. planner for mobile robots
    • 현실에서 모바일 로봇을 위한 planner가 성공적으로 배치된게 존재한다. 
      비록 그들이 multi-goal mission으로 디자인하것이 아니지만, 우리는 이전에 입증된 개념과 디자인 패턴을 사용할것이다.
    • 우리의 연구는 두갈래로 나누어진 global과 local planning구조를 채택하였다. 
      local planner는 로봇 주변의 자세한 정보를 가지고, 장애물을 피한다.
      global planner는 coarser paths를 따라간다.
    • 이러한 구조를 따르면, 우리는 완전한 경로를 생성하고 사용하며, local가 높운 주기로 경로를 재조정한다.
    • 이산 volumetric map은 흔히 환경을 나타내기 위해서 사용된다. ( 이는 Volxblox로 생성 )
    • 기존의 연구들에서는 환경과의 부피적 충돌을 고려했지만 주행 가능성은 반영하지 않았다.
      아는 local planner에게 경로의 안전성에 매우 중요한 요소다.
      그러므로 우리는 보행로봇의 모듈을 활용한다. global planner에서. 그리고 이를 가지고 로봇의 주행가능성을 평가한다.

 

 

3. problem statement

  • 우리는 multi-goal mission에서 모든 ToI를 방문하는 안전한 global path를 찾는 문제를 해결하는것이 목표이다.
    • 우리는 문제는 MTP문제로 공식화했다. 
    • 로봇은 주변의 multiple PoIs에서 하나의 ToI에 방문할수있다.
    • 본 연구에서는 ToI가 하나의 PoI만 방문하게 제한한다.
    • PATH는 이산적인 waypoints의 집합이다.
      • waypoint : 로봇이 경로를 따라 이동할때 거쳐야하는 중간지점을 의미

인자들에 대한 설명

 

set of waypoints

 

경로 구간 path segment
비용함수............................경로구간이 주어지면, 경로구간의 비용cost는 다음과 같은 양의 부호를 가진 함수로 정의
path W가 주어지면, 모든 path segments의 cost합은 위와 같이 정의한다.

  • 문제에 대해서 입력과 출력을 요약하면 아래와 같다.
    • ==> 입력

start and end pose
A set of ToI poses
p i j는 목표지점 t i에 대해서 j번째 PoI를 의미

  • =====> 출력 

위의 조건을 우선 만족해야한다.
출력은 충돌없는 최소비용의 경로이다.

  • 본 연구에서는, 상태 공간 C는 SE(2)이다. 이는 기어다니는 로봇들에게 적절하다.
    • SE(2) : special euclidean group in 2D이다. 2D공간에서의 위치와 방향을 표현하는 수학적 공간이다.
      • position은 (x,y)로 나타내며 2D 평면상의 좌표이다.
      • rotation은 회전이다.(방향) Yaw  ψ
        • SE(2)공간에서 하나의 state는 ( x , y , ψ )로 표현한다.
  • 하나의 state를 의미하는 s는 아래의 식처럼 표현할것이다.

보기 편하게 전치 시킴 ( 식 a )

  • 비용함수 C(  ● , ● )는 Open Motion Planning Library (OMPL)의 기본 거리 함수를 사용할것이다.
    (당연 SE(2)공간에서...)

다음과 같은 함수이다.

 

 

 

 

위의 식에 대한 설명1
위의 식에 대한 설명 2

 

 

 

회전 각도 차이를 구하는 함( 두 각도 간의 최단 거리를 찾기 위해서 두값을 비교해서 최솟값을 선택함. )

 

기타 설명1
기타 설명 2

 

 

 

 

 

계산 예시

 

 

 

 

SMUG planner에 대한 개요.... Fig.2
Fig. 3. traversability map은 0과 1사이 범위로 지정되며, 색상은 red에서 blue로 변한다. d는 tlow=0.3 , thight=0.8로 지정하여 분할한 결과이다. 높은 값은 초록색, 낮은 값은 빨건색이며, 중간값은 보라색이다.

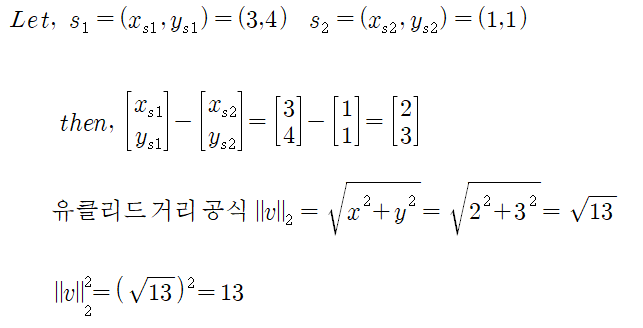
4. METHOD

  • MTP ( multi-goal path planning)을 직접적으로 해결하려면 collision-free path의 수가 너무 많다.
    • 그러므로 본 연구에서는, 2-step의 method로 나누어서 풀기로 결정하였다. ( [29]도 이와 같은 방식을 취하였다.)
    • First Step
      • ToI를 방문하는 최적의 순서를 TSP를 사용하여 simplifying하였다. 
        • 이러한 simplification은 PoIs가 해당되는 ToI와 가까운 경우에만 유효하다.
    • Second Step
      • 각각의 ToI에 대해서 total path cost를 최소화하는 PoI를 선택한다.
  • Fig.2
    • 1. optimal path planner는 2개의 states를 연결하는 최적의 경로를 생성한다. ( 섹션 4-A )
    • 2. planning을 하기 전에 우선 state validity checker를 사용한다. ( VoxBlox의 Truncated Signed Distance Field (TSDF)와 traversability map을 사용해서... ) ( 섹션 4-B)
      • grid world로 비유하면 못가는 grid인지를 판단하는것. 단 여기에서는 격자 하나가 아니라 로봇의 형태,크기,동장,특성등을 고려해서 보다 더 정교하게 평가한다.
      • TSDF란?
        • 절단 부호 거리 함수이다. 즉, 3D공간에서 물체와의 거리를 저장하는 방식
        • TSDF는 각 지점(voxel)에서 가장 가까운 표면까지의 거리를 저장하는 3D맵이다.
          • 만약 거리값이 양수라면? ==> 장애물 표면에서 떨어져있음
          • 만약 거리값이 0이라면?  ==> 장애물 표면 바로 위에 있음
          • 만약 거리값이 음수라면? ==> 장애물 내부에 있음 ( 충돌 가능성이 높으니 위험 지역이다. )
    • 3. TSP solver는 cost matrix를 가지고 ToIs의 최적의 방문 순서를 계산한다. ( cost matrix는 각각의 ToIs간의 path cost를 가지고 있다. ) ( 섹션 4-C)
    • 4. IDP module은 각 ToI간의 최적의 PoI를 선택한다. ( 선택하는 방식은 total path cost를 최소화 하는 방향으로 )  ( 섹션 4-D)
    • 5. local planner는 입력받은 global path를 따라서 정교한 local path를 생성한다.
  • 4-A . optimal path planning
    • informed sampler와 LazyPRM*를 사용하여, 2개의 state 사이의 최적의 collision-free path를 생성한다.
      • sampler는 SE(2) 공간에서 균일하게 sample을 생성한다. 
        initial path를 발견하고, sample space는 cost function과 current path cost를 기반으로 제한하여, path 최적화에 가속한다.
        informed sampler는 L2 cost를 기반으로하여, 새로운 cost function을 구현하였다. ==>  C(  ● , ● )
        • L2 cost는 보통 'L2 norm노름'을 사용한 비용함수이다. L2 norm은 유클리드 거리라고도 한다.
      • path가 state s1에서 시작하고 state s2에서 끝난다고 가정합니다. 그리고 initial path의 cost가 이미 구해져있다고 가정합니다. 그러면 새로운 샘플 S new 는 타원 모양 안에서 생성됨니다. 그러면 타원밖에 존재하는 샘플 s는 cost를 개선할수 없습니다. 이는 아래의 방정식에 따름니다.

새로운 샘플을 생성하기 위한 범위. 두점 s1과 s2로부터의 거리 제곱의 합이 일정한 값은 C0 - Cr보다 작은 값들이 타원 내의 sample들이다.
식 4-A-1. '공간적 거리 비용' + '방향/각도 차이 비용'

 

식 4-A-2 .
식 4-A-3

  • 그리고 yaw angle인 ψ s new는 [−π,π] 범위에서 균등하게 샘플링 된다. 절차는 아래와 같다.
    • 그리고 sampling된 states는 state validity checker로 전해져서, 환경과의 충돌을 피하게 한다.

 

 

  • 4-B . state validity checker
    • 우리는 계층적 obstacle avoidance scheme를 사용하여, 안전하고 실행 가능한 path를 효율적으로 생성합니다. 
    • 우리는 로봇에 특화된 traversability module을 채택해서 시뮬레이션 합니다. 이로 인해서 명확히 안전한 state는 받아드리고, 명확히 안전하지 않은 것들은 버림니다.
      • 오직 안전성이 불확실한 state만 iterative volumetric fashion으로 collision 검사를 합니다.
    • 4-B-1 . Traversability Filtering
      • 우리는 CNN으로 학습된 traversability map을 사용합니다. 이것은 occupancy map을 입력받습니다.
      • 네트워크는 시뮬레이션에서 각각의 voxel에 대해서 traversability를 0~1사이로 추정하여 할당합니다. 할당하는 기준은 traversing 성공률을 기준으로 합니다.
        우리는 해당 모듈울 사용해서 충돌 검사 양을 줄여줍니다. 
        •  (  voxel( volume + pixel )은 3차원 공간에서 최소 단위로, 3D픽셀이라고 생각할수있다. 마치 2D이미지에서 픽셀이 색상 정보를 가지듯이, voxel은 3D공간에서 위치와 속성을 가지는 작은 큐브 단위 이다. )
      • traversability는 2개의 설정된 threholds에 따라서 3 level로 나누어진다. ( 임계값은 low , high이다. 그리고 이 값들은  0 <= low <= high <=1 을 만족한다. )
      • 우리는 연속적인 traversability의 상태를 식a에서 정의한대로 해당되는 traversability voxel을 쿼리를 통하여 얻는다.
      • traversability가 low보다 낮은 state는 무효화가 된다. 그리고 high보다 높다면 유효함으로 한다.
        오직 low와 high사이의 traversability 만 collision-check를 수행한다.
        • 이는 분명히 유효 or  무효한 상태에 대해 collision-check를 피하게 해준다.
    • 4-B-2 . Volumetric Iterative Collision Checking
      • 명확하지 않은 traversability  지역에 대해서, 우리는 robot의 bounding box에 대해서 iterative volumetric checking에 의지한다.
      • Voxblox에서 생성한 TSDF를 사용해서, box가 환경과 충돌을 하는지 체크한다. 
        이를 위해서, 상자 중심에서 가장 가짱운 환경 표면까지의 거리를  TSDF맵에서 얻고, 이를 상자의 외부 및 내부 구체 반지름과 비교한다.
        • 만약에 거리가 내부 구체의 반지름보다 작다면, 상자는 충돌하는 것으로 간주함.
          만약에 거리가 내부 구체의 반지름 보다 크다면, 상자는 충돌안하는걸로 간주한다.
          그렇지 않으면 결론을 내지않는다. 즉, 두 기준 사이에 존재하면, 결론을 내기 어려우니 상자를 더 작은 부분들로 나눈다.
          그리고 각 상자에 대해서 같은 과정을 반복해서, 충분히 작은 작위에서 충돌 여부를 판단한다.
          • 만약에 최소 하위 상자까지에도 도달할때까지도 결정이 안되면 충돌 여부는 외부 구체(가장 처음에 사용한 구체)만 사용한다.

 

  • 4-C . Optimal Sequencing ( TSP )
    • ToIs의 최적의 방문 순서를 찾기 위해서, 우리는 우선 모든 ToIs간의 collision-free path를 생성할것이다. 결과로써 아래와 같은 cost matrix가 생성된다.

생성된 cost matrix

  • 그리고 아래의 식과 같이, 비용을 최소화 하고자 한다.

촤소화 시켜야함

 

  • 4-D . Iterative Dynamic Programming
    • 방문 순서가 결정된 이후에,  planner는 각각의 ToI에 대해서 PoI를 선택한다. 
    • 2개의 연속적으로 방문된 ToI간에(방문 순서상 서로 이어지는 두 개의 ToI) , 모든 PoI 사이에서 collision-free path가 주어질때, 최적 경로 비용을 찾기 위해 아래와 같은 DP를 사용한다.
      • ( 즉 2개의 서로 떨어져있는 지점으로 가기 위해서 중간에 거치는 노드들이 많을거임. 이때 충돌이 없는 모든 가능한 경로를 '모든 PoI'라고 한다. 이제 가기 위해서 어떻게 PoI를 거쳐서 지나갈지 찾아야하는데, 이러한 최적의 경로 비용을 DP를 이용한다는 것. )

식의 인자에 대한 설명들

 

최적의 경로 비용을 찾는 DP

 

DP 과정 1

 

DP 과정 2
DP 과정 3. 시작점 s에서 출발해서 마지막 목표까지 도달하는 최적비용
최적의 PoIs를 선택해서 위와 같은 것을 얻는다.

  • DP는 두개의 연속적으로 방문된 ToI간의 모든 PoI 간 경로가 주어지면 global optimum을 출력하는 것이 보장된다.
  • 하지만 N개의 ToI와 각 ToI에 대해서 M개의 PoI가 존재할때, ( 즉, | T | = N이며 | P i | = M일때를 의미 ) 
    M*M( N-1 ) + 2M개의 충돌이 없는 경로를 계획해야하니 PoI의 수에 따라서 path plan이 제곱급으로 증가한다.
  • 결국에는, 최적의 global path를 구성하는데 사용되는 path는 모든 path가 아니다. 그래서 우리는 반복적으로 DP를 사용하고, 각 반복후에 최적의 global path를 구성하는데 필요한 경로만 collision-free path로 계획하는 방법을 제안하다..

  • 위의 식은 pi와 pj 사이의 충돌 없는 경로 W( pi , pj )의 경로 비용이다. 
    만약에 경로가 이미 계획되어 있다면, 해당되는 경로 비용을 사용한다.
    그렇지 않다면 , l( pi , pj )는 와 사이의 직선 경로를 사용하여 의 실제 비용을 근사한 값이다.
    • 즉, c( pi ,pj )는 위에서 설명한  (OMPL)의 기본 거리 함수를 사용해서 비용을 구할 것이다. 그리고 이는 W( pi , pj )의 경로 비용의 하한선이다.
  • 각각의 반복에서 우리는 이전에 소개한 DP를 수행하는데, 여기에서는 cost( W ( . , . ) )을 l ( . , . )로 교체해서 PoI를 찾는다. 그 후에는 2개의 연속적으로 방문한 PoI를 연결하는 collision-free path를 생성하고 그에 따러서 l을 업데이트 한다.
    • 알고리즘은 선택된 PoI가 반복마다 변경되지 않으면 종료된다.
  • 이렇게 함으로써 M*M( N-1 ) + 2M개의 collision-free path를 생성할 필요가 없어서 전체 계획 시간이 줄어든다.
    • 이러한 DP방법은 동일한 PoI에서 PoI로 가는 path가 주어진 경우에, 결과 경로 비용이 다른 가능한 경로들의 하한선보다 낮기 때문에 DP의 최적성을 유지한다.
  • 마지막으로, 우리는 얻어지 ToI의 순서와 선택된 PoI에 따라서 path segment를 연결한다. 각 waypoint의 방향을 경로 방향에 맞게 정렬하는데, PoI에서의 waypoint는 고정되어 있으나 나머지 waypoint들은 로봇이 옆으로 이동하는 대신에 앞으로 이동하도록 방향을 맞추어 준다.

 

 

 

5. EXPERIMENTS

  • 본 실험에서는 달표면 환경과 실내 공간을 커스텀하여 시뮬레이션 한다. ( 이는 탐험과 산업현장에서의 가능성을 보여준다.)
  • 달 환경에서는 13개의ToIs가 존재하며, 각각은 주변에 균등하게 10개의 PoIs가 생성된다.
  • 실내 환경에서는, 12개의 ToIs가 존재하며 각각은 2개의 PoIs를 선택하여서 더 작은 크기의 문제를 나타낸다.
    • Fig6은 두 환경에 대해서 생성된 경로를 보여준다.
    • 이 문제를 해결할 수 있는 다른 방법이 존재하지 않기에, 우리는 제안된 방법을 우리가 설계한 기준선 방법과 비교한다.
      • 이 실험은 laptopwith IntelCore i7-9750HCPUand32GBRAM 에서 하였다.
      • 모든 평균값과 표준편차는 1-번의 연속 실행을 기반으로 계산된다.
  • 1) IDP/DP/ IterativeRubberBandAlgorithm(IRBA) Comparison
    • 우리는 IDP의 성능을 DP로 전부 m^2(N-1) + 2M의 충돌 없는 경로를 사전에 계획한후, DP를 한번 실행하는 방식과 비교하고, MTPGR를 하기 위해서 제안된 방법을 적용한 Iterative Rubber Band Algorithm (IRBA)과 비교한다.
    • IDP와 IRBA은  m^2(N-1) + 2M 경로를 모두 계획할 필요가 없기 때문에, 계획 시간이 크게 줄어듭니다. 표 1에서 볼수 있듯이, 13개의 ToI와 각각 10개의 PoI가 있는 달 환경에서는 DP는 두번째 단계에서 1220개의 충돌없는 경로를 계획해야하며, 평균 71.87초를 소요한다.
      반면에 IDP는 평균 8.05초만에 끝나며, 계획 시간을 88.80% 절약하고 8.9배 빠르다.
      실내 환경에서는 12개의 ToI와 각각 2개의 PoI가 있을 때, DP는 48개의 충돌 없는 경로를 사전에 계획하고 평균 7.59초를 소요하며, IDP는 7.20초를 소요해 계획 시간을 5.1%만 절약다. 이는 PoI 수가 적기 때문이다.
      IRBA와 IDP는 계획 시간 측면에서 거의 동일한 성능을 보이며, 두 환경에서 차이는 각각 8%와 3%의 표준편차 범위 내에 있다.
    • 경로 비용 측면에서는, IDP는 두 체스트에서 DP와 유사한 비용을 생성한다. 그 차이는 DP가 더 많은 경로를 계획하면서 더 밀집된 그래프를 구축하기에 발생한다.
      그러나 IRBA는 DP에 비해 경로 비용을 2-3% 증가시키며, IDP에 비해 이론적인 최적성 보장이 없다. 따라서 환경에 따라 IRBA와 IDP 간의 성능 차이가 더 클 수 있다. 
      동일한 그래프에서 실험을 진행할 경우, IDP는 섹션 IV-D에서 설명한 대로 DP와 동일한 경로 비용을 생성하며, IRBA는 종종 더 나쁜 결과를 생성한다.

표1